videos que te pueden servir .


www.youtube.com/watch?v=cQH5FGF7m8c

www.youtube.com/watch?v=MvBH3qiy_7g

www.youtube.com/watch?v=zlM-m7Y-o6A

www.youtube.com/watch?v=5MhS-qLyFmo

www.youtube.com/watch?v=sj_gU_EAhdU

punto de reflexión

Cuando una imagen se refleja a través de un solo punto en lugar de una línea de simetría, esto se conoce como "punto de reflexión". El centro de la figura es un único punto. Para cada punto en un lado de la figura, hay un punto correspondiente en el lado opuesto del punto de reflexión. Con un punto de reflexión, la imagen resultante es congruente con la imagen original.

para saber mas :  

Una reflexión se refiere al cambio que se hace en la matriz de la función, también la podemos llamar transformación.

Para que se de una reflexión tomamos la matriz de la función ya sea f(x)=A sen (bx+c) + d,o cos en su mismo orden.

Y lo que hacemos es alterar uno de los valores un ejemplo de ello si A vale 2Π podemos cambiarla a -2Π lo que significaria una reflexión en alguno de los ejes según el valor positivo o negativo que le demos a Y,que es lo mismo 

Eje de simetría

	El eje de simetría (también llamado eje especular) no tiene por qué ser vertical ni horizontal, puede ir en cualquier dirección. Pero hay cuatro direcciones comunes, sus nombres vienen de las líneas que denotan en un gráfico estándar X

tipos de reflexión

Reflexión simétrica :

Hay tres tipos de simetría: la simetría reflexiva, la rotación y la traslación .  La reflexión simétrica también se conoce como especular o simetría lineal.

Reflexión horizontal :

Cuando una imagen reflejada se da vuelta horizontalmente, es un reflejo horizontal. Una figura con simetría horizontal tiene un eje vertical de reflexiodad. Las dos partes del cuerpo humano son un reflejo horizontal el uno del otro. El cuerpo humano tiene un eje vertical de reflexión. Cuando se imprime la letra mayúscula "A" tiene un eje vertical de reflexión y, por lo tanto, es un ejemplo de un reflexión horizontal.

Reflexividad vertical

Si una forma se voltea verticalmente, es un reflejo vertical. Las figuras con simetría vertical tienen un eje horizontal de reflexión. Cuando se imprime la letra mayúscula "E" tiene un eje horizontal de reflexión y es un ejemplo de un reflejo vertical. Una forma regular de diamante es un ejemplo de un reflejo vertical y tiene un eje horizontal de reflexión.

Reflexión  lineal :

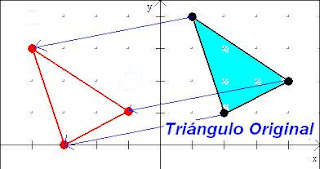
En una reflexión lineal, la preimagen -o imagen original- se refleja a través de una línea de simetría en forma de una imagen. Cada punto de la imagen es la misma distancia desde la línea de reflexividad como el punto correspondiente de la imagen original. El resultado es una figura que es congruente con la imagen original conocida como isometría. Que sea congruente significa que las dos formas son del mismo tamaño, los ángulos son iguales y los segmentos de línea son de la misma longitud. La imagen de una persona en un espejo es una reflexión lineal.

EL PRICIPIO DE LA REFLEXIÓN.

Principio de reflexión

En teoría de conjuntos, una rama de las matemáticas, el principio de reflexión dice que es posible encontrar conjuntos que representen la clase de todos los conjuntos. Existen varias formas diferentes del principio de reflexión según se determine con exactitud el significado de «representar». La forma débil del principio de reflexión lo constituyen los axiomas de Zermelo-Fraenkel, mientras que formas más fuertes pueden resultar en axiomas nuevos y muy poderosos para la teoría de conjuntos.

El concepto de «principio de reflexión» proviene del hecho de que las propiedades del universo de todos los conjuntos se «reflejan» en un subgrupo más pequeño.

El principio de reflexión como teorema de ZFC.

Tratando de formalizar la argumentación de la sección anterior para el principio de reflexión dentro de los axiomas de Zermelo-Fraenkel, se vuelve necesario agregar algunas condiciones a la colección de propiedades «A» (por ejemplo, «A» debe ser finita). De esta manera se generan varios teoremas de reflexión de ZFC fuertemente relacionados, todos los cuales establecen que podemos encontrar un conjunto que será al menos modelo de ZFC.

Una forma del principio de reflexión dentro de ZFC establece que «para cualquier conjunto finito de axiomas de ZFC podemos encontrar un modelo que implícitamente satisfaga tales axiomas». (en particular esto prueba que ZFC no es axiomatizable en forma finita, porque si se probara la existencia de un modelo de sí mismo y, por tanto, que demostrara su propia consistencia, tal posibilidad contravendría el segundo teorema incompleto de Gödel), esta versión de teorema de reflexión está muy relacionada con elteorema de Löwenheim-Skolem.

Otra versión del principio de reflexión dice que para cualquier número finito de fórmulas de ZFC podemos encontrar un conjunto V_α en el universo de von Neumann tal que todas las fórmulas en el conjunto constituyen un absoluto lógico para V_α (lo que significa muy burdamente que verifican en V_α si y solo si lo hacen en el universo de todos los conjuntos). Así se establece que el conjunto V_α refleja el universo de todos los conjuntos, al menos en lo que concierne al número finito de fórmulas dadas.

Para cualquier número natural n, puede probarse desde ZFC un principio de reflexión que dice que dado un ordinal α, existe un ordinal β>α tal que V_β satisface todas las instancias de primer orden de la teoría de conjuntos que son verdaderas para V, y contienen menos que n cuantificadores

REFLEXIÒN

El tártago de la hoja cerrada es un aplana nativa de Europa, que crece de manera silvestre en praderas y caminos. Por la forma en que se agrupa sus hojas, el tartádo se caracteriza por poseer varios ejes de simetría.

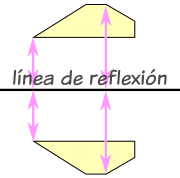
Una reflexión es una transformación geométrica. En una reflexión, un objeto geométrico “se mueve de un tirón” a través de una recta. La recta a través de la cual se refleja un objeto se llama la recta de reflexión o el eje de la reflexión.

El manipulante 1 demuestra la reflexión de un pentágono irregular a través de una recta. Chasque encendido los puntos azules en el manipulante 1 y arrástrelos para cambiar la figura. Observe que la figura reflejada es una imagen de espejo de la figura original. Para ver la construcción de A y deB', chascar encendido las cajas de cheque.

Características de reflexiones

• Un objeto y su reflexión son simétricos sobre la recta de reflexión.
• Un objeto y su reflexión son congruentes.
• Un objeto y su reflexión son similares.
• Si un objeto reflejado es otra vez reflejada recta casi igual de reflexión, el objeto resultante es coincidente con el objeto original.

Para hacer una reflexión es necesario determinar la recta a tráves de la cual se a reflejar la figura. Esta recta actua como un espejo, donde se ve el reflejo de una figura dada y se denomina eje de reflexión o de simetría.

 

https://www.youtube.com/watch?v=cQH5FGF7m8c